大致按涩情程度从小到大排序。最后面的题最好玩。
蓝桥杯 组合数问题
Statement
给 $n,m,k$,求有多少对 $(i,j)$ 满足 $1 \le i \le n,0 \le j \le \min(i,m)$ 且 ${i\choose j} \equiv 0\pmod{k}$,$k$ 是质数。
$1 \le n,m \le 10^{18}$,$1 \le k \le 10 ^ 8$,多测 $10 ^ 5$ 组数据。
Solution
Hint 1
卢卡斯定理。
Solution
应用卢卡斯定理,可以得到 ${i\choose j} \equiv \prod \limits _{t = 0} {i _ t \choose j _ t} \pmod k$,其中 $i _ t, j _ t$ 为 $k$ 进制下 $i, j$ 的第 $t$ 位。也可以得到,其值为 $0$ 当且仅当某一位 $j _ t > i _ t$。
于是做数位 dp 即可,维护当前 $i$ 和 $n$ 的关系,$j$ 和 $m$ 的关系,转移时要求 $j _ t \le i _ t$。细节比较多,但是状态很少,可以上各种各样的矩阵优化 dp 办法(当然这个题不行)。
什么你问为什么这种题都能出现在这里,其实是因为初见杀。
CF317E Princess and Her Shadow
Statement
平面直角坐标系上,有一个公主和她的影子,还有 $ m $ 棵树,公主在 $ (v_x,v_y) $,影子在 $ (s_x,s_y) $。
公主要去追影子。
公主向右走,影子就会向右走;公主向左走,影子就会向左走;公主向上走,影子就会向上走;公主向下走,影子就会向下走。
如果影子前进的方向是一棵树,影子就不会动。公主不能撞树。
求一组公主的行动方案,让公主抓到影子,要求方案长度不能超过 $ 10^6 $ 。若无解,输出 -1。
$0 \le m \le 400$,坐标范围均在 $[-100,100]$ 内。
Solution
Solution
无解条件是公主和影子不在一个连通块内。
若公主和影子和外部连通,那么可以搜一条路径把公主移动出来,再移动远一点。再搜一条路径,把影子移动出来,然后找到最靠上(或者靠下)的把公主和影子的纵坐标对齐,然后类似的横坐标对齐。
否则,让找一条公主到影子的路径,公主沿着这个走,走完之后再沿着影子走的路径走。这样能构造出来的证明:当公主走到当前影子的位置时,假如影子撞了树,距离就会变近;如果没撞树,影子就会相应的向那个方向移动一段距离,这个过程不可能无限下去,因为内部空间有限。
蓝桥杯 铺瓷砖
Statement
用如下两种形状的瓷砖铺满一个 $n \times m$ 的矩形,求方案数对某固定数字取模的结果。
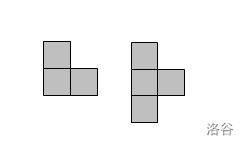
$1 \le n \le 10 ^ {15}$,$1 \le m \le 6$。
Solution
Solution
对于某一种放置瓷砖的方案,考虑钦定一个放置的顺序。可以考虑按照瓷砖的左上角的位置(在这里认为瓷砖不可以旋转),从上到下再从左到右排序去放置,这样每种放置位置和顺序就和一种放置方案一一对应了。就可以写出一个爆搜:每次放置一个瓷砖,然后递归下去。
考虑优化这个爆搜,可以发现在第 $i$ 行填满前,第 $i + 3$ 行不会有被覆盖的位置,于是如果设计 dp 状态为 $f _ {i, S}$ 为前 $i$ 行填满了并且接下来两行的状态为 $S$,那么它是可以转移的。搜索转移的时候必须填满这一行之后再删去这一行并添加一条转移边。
不过 $2 ^ {2m}$ 很大,可以从 $S$ 为空开始搜索转移,建图,然后再从 $S$ 为空开始对反图 bfs,只取两次搜索都能到达的状态。这样优化之后只剩下了 $236$ 个状态。
一些更多的优化:观察到对称的状态的值一定一样,于是可以合并,入边只保留其中一个的,出边不变。这样优化之后只剩下了 $126$ 个状态。
矩阵快速幂优化 dp 即可。
请问您今天要来点取模吗?
Statement
给定长为 $n$ 的数列 $a$。对于一个非负整数 $x$,定义函数 $f(x) = x \bmod a _ 1 \bmod a _ 2 \bmod \cdots \bmod a _ n$(即先对 $a _ 1$ 取模,再对 $a _ 2$ 取模,一直取模到 $a _ n$)。
给出非负整数 $l, r$,求 $\sum \limits _ {i = l} ^ r f(i)$ 的值对 $10 ^ 9 + 7$ 取模的结果。
$1 \le n \le 10 ^ 5$,$0 \le L \le R \le 10 ^ {18}$,$1 \le a _ i \le 10 ^ {18}$。
Solution
Hint 1
$x$ 取模之后,要么值不变,要么值至少减半。
Solution 1
先把 $a _ i$ 找到一个前缀最小值序列,只有这些位置的值可能有用。
考虑如何计算一个值域前缀 $x$ 的答案:找到第一个小于等于它的 $a _ i$,分解成一些 $a _ i - 1$ 和一个 $x \bmod a _ i$。这启示我们从后往前计算不断 $a _ i - 1$ 的答案,每个只要 $O(\log n\log V)$ 的复杂度。
对于查询,如上所述,进行一次也是 $O(\log n\log V)$ 的。
Solution 2
从前往后枚举时,用优先队列维护现在要求的一些前缀 和它们的系数。每次新来一个 $a _ i$,就不断弹出前缀位置大于等于 $a _ i$ 的,设为 $x$,将其分解成一些 $a _ i - 1$ 和 $x\bmod a _ i$。然后将所有的前缀 $a _ i - 1$ 的系数求和合并起来,这样被加入的非取模后的数只有 $O(n)$ 个,而它们每个最多只会被取模 $O(\log V)$ 次,总的复杂度就是 $O(n\log n\log V)$。
CF521D Shop
Statement
- 有 $k$ 个正整数 $a_{1\dots k}$。
有 $n$ 个操作,每个操作给定正整数 $t, i, b$,有三种可能:
- 如果 $t = 1$,这个操作是将 $a_i$ 赋值为 $b$;
- 如果 $t = 2$,这个操作是将 $a_i$ 加上 $b$;
- 如果 $t = 3$,这个操作是将 $a_i$ 乘以 $b$。
- 你可以从 $n$ 个操作中选择最多 $m$ 个操作,并按照一定顺序执行。
- 你的目标是最大化 $\prod_{i=1}^k a_i$ 的值。
- $k,n \le 10^5$。
Solution
Solution
jiangly 写的太好了我还要写吗,是不是写一下好一点。
确定操作后顺序一定是赋值、加、乘。每个位置赋值最多一次,转化成加法。加法从大到小,转化成乘法。排序即可。
真的很聪明吧!
「eJOI2021」Waterfront
Statement
给定 $N, M, k, x, h[1, \cdots, N], d[1, \cdots, N]$。
有 $N$ 棵灌木,初始高度为 $h$,有 $M$ 天,每天第 $i$ 棵灌木高度会先增长 $d _ i$,之后园丁可以对某些灌木共修改不超过 $k$ 次。
每次修改可以选定灌木 $i$,要求当时 $i$ 的高度大于等于 $x$,随后将其高度减小 $x$。
求最后最高的灌木的最小可能高度是多少。
$1 \le N, M, x \le 10 ^ 4$,$1 \le k \le 10 ^ 3$,$0 \le h _ i, d _ i \le 10 ^ 4$。1s。
Solution
Hint 1
贪心。
Solution
好像乱斗一下就做完了!
考虑一个贪心,先尝试砍最后最高的灌木。能砍就一定砍它,砍不动了就可以直接得到答案。
问题在于什么时候砍。其实,尽量靠前的砍是最优的。可以调整法证明。
于是可以维护每天已经用掉了多少次砍,每个灌木一个指针表示目前从哪天开始可以被砍。
每次找到最后最高的那个灌木,移动其指针,砍它。这个过程不超过 $Mk$ 次。移动指针最多有 $NM$ 次。
复杂度 $O(NM + Mk\log N)$。
代码。你怎么胡题还写代码啊。
JOISC 2017 Broken Device 2
Statement
这是一道通信题。
你需要实现两个函数 void Anna(int N,long long X,int K,int P[]) 和 long long Bruno(int N,int A[]) 来实现以下功能:
Anna将得到一个长为 $N=150$ 的空白序列和一个不大于 $10^{18}$ 的数字 $X$,这个函数需要为每一位赋予一个 $0$ 或 $1$ 的值来保存 $X$,其中序列中有 $K$ 个位置是损坏的:无论设置为 $0$ 还是 $1$,这些位置的值都恒为 $0$,$P$ 数组保存着这些位置的下标;Bruno将得到Anna操作后的序列,这个函数需要依靠这个序列来还原Anna得到的数字 $X$。
$K \le 40$。
Solution
Hint 1
以两位(或者三位)为单位保存信息。
Solution
用三位为单位保存信息是正解,可以参考洛谷题解。这里是乱搞。
首先,考虑将长度 $150$ 的序列每两位分一段,每一段若有一个位坏掉就都是 $0$(称之为坏段),否则以三进制存储信息。这样的话,最多能有 $40$ 个坏段,则只能表示出 $3^{35}$ 级别的数,显然无法通过。
考虑随机化:让 Anna 和 Bruno 都使用同一个随机排列来遍历数组。我采用的是标准库里的 mt19937,如果种子一样,生成的序列也一样。也可以直接打表出一个随机排列。
这样可以使一些坏段拥有两个坏位,就减少了坏段的数量。期望懒的算了,但是这样就可以获得 $90$ 分,通过 $L \le 38$ 的测试点。
考虑将坏段利用起来:如果一个坏段有一个好位,并且将这个好位置为 $1$ 时,它和 $X$ 当前三进制最低位的表示恰好相同,那么就可以利用上这个坏段表示三进制的一位。
期望还是懒的算了,但是这样就可以通过。因为是随机的顺序,所以 $K$ 一定时任何数据对它都是一样的,所以能反映出它正确率是很高的。
在代码实现中,三进制的表示为 $0 \to 10$、$1 \to 11$、$2 \to 01$。
代码。
如果我这样实现的话,当 $X$ 在三进制下全是 $1$ 的时候就会爆炸;避免的方法是对于每一个位置,设置一个只关于它的随机函数,三进制下随机映射这三种即可。但是数据水冲过去了。
CF1889D Game of Stacks
Statement
有 $n$ 个栈,每个栈里面包含若干个 $1$ 到 $n$ 的数字,
你想要知道 $\text{init}(1\sim n) $ 的值。
函数 $\text{init}(i)$ 的定义是:先初始化 $n$ 个栈为初始状态,然后调用 $\text{get}(i)$,$\text{get}(i)$ 的定义是:取出第 $i$ 个栈栈顶数字并将其弹出栈,并将该数字作为新的 $i$ 递归执行 $\text{get}(i)$,直到某个栈取出数字失败,返回该栈的编号作为的最终答案。 需要注意的是,每次执行 $\text{init}()$ 函数都会将栈复原,因此 $n$ 次函数调用都是独立的。
$1 \le n \le 10^5$,每个栈初始包含的数字在 $1$ 到 $n$ 之间,包含的数字总个数 $\le 10^6$。
Solution
Hint 1
从某个点开始,如果走一段后第一次回到这个点,那么这相当于把环上每个点都弹一个栈顶。
Hint 2
无论从哪里开始,一个环都会被弹一次栈顶,然后回到起点。
Solution
环的弹出是无论如何都会被弹出的,所以遇到环就直接弹出就好了,之后就会形成一个森林。不断找环弹出是比较难的,但是可以直接在搜索过程中弹出环,这样总的复杂度是 $O(n + \text{栈内数字个数})$ 的。
是很有趣的,Ad-hoc 的性质(?)
ICPC WF 2009 E Fare and Balanced
Statement
有一张 $n$ 个点 $m$ 条带权边的有向无环图,保证每条边都能由点 $1$ 到达,也能到达点 $n$。
现在要把一些边的权值增加,使得从 $1$ 到 $n$ 的所有路径的权值和都相等并且尽量小。并且要求对于任意一条路径,其上不能有多于一条边的权值增加。
判断无解或给出解。
$1 \le n, m \le 5 \times 10 ^ 4$。
Solution
Solution
定义 $U(u, v)$ 表示 $u$ 到 $v$ 的所有路径的权值和是否全部相同,$u \rightsquigarrow v$ 表示 $u$ 到 $v$ 的路径,$u \to v$ 表示 $u$ 到 $v$ 的一条边。
先假设 $U(1, n)$ 为假,不然不用修改。
性质 1:若存在 $v$ 使得 $U(1, v)$ 和 $U(v, n)$ 都不成立,则无解。证明很容易,因为如果有解,就一定要修改 $1 \rightsquigarrow v$ 和 $v \rightsquigarrow n$ 两部分路径上各至少一条边,于是不符合题面要求。
性质 2:如果 $U(1, u)$ 为假且存在 $u \to v$,那么 $U(1, v)$ 为假。
于是,考虑所有满足 $U(1, u)$ 为真且 $U(1, v)$ 为假的一条边 $u \to v$,只需要将这些边增加权值使得经过这条边的最长路的权值和与原本的最长路权值和相等即可。
首先是证明这样一条路径上不会有两条边:一条路径上一定是前半部分 $U(1, u)$ 为真,后半部分 $U(1, v)$ 为假,那么一定恰好有一条边是这样的。
其次,由于 $U(1, u)$ 为真且 $U(v, n)$ 为真,所以可以知道原本经过这条边的任意一条路径的长度是确定的,于是可以直接增加这条边的权值。
「eJOI2021」Dungeon
Statement
你需要在一个 $N \times M$ 的地图进行游戏。地图的每个位置包括下列类型:空地、墙壁、金币、炸弹和起始位置 $\texttt S$。
每张地图包含一个或多个 $\texttt S$。当游戏开始时,你的起点将会被选定为任意一个 $\texttt S$。由于地图视野较暗,因此你只能看到以自身为中心的 $3 \times 3$ 正方形内的位置。同时,炸弹和起始位置在视野中会被视为是空地。注意,你不可以进入墙壁。
你每一步可以向上下左右四个方向进行移动。当你进入金币格时,你会获得 $1$ 枚金币,同时该格的金币消失。当你进入炸弹格时,你失去所有金币且游戏结束。
保证第一行,第一列,最后一行和最后一列只包含墙壁。
你获得了地下城的地图。然而你不知道你的起点会是哪儿——但是保证你会从某个起点出发。求如果你以最优策略进行游戏,最坏情况下能够获得金币数量的最大值。
设地图中起始位置的数量为 $S$。
有意义的部分分:$S = 1$、$N, M \le 250, S \le 12$。
总的数据范围:$1 \le N,M \le 400$,$1 \le S \le 60$。
Solution
Hint 1
你先做部分分。
Solution
虽然并没有独立做出来但感觉这题很有趣所以还是放上来了。
考虑 $S = 1$:我知道我在哪里!直接避开所有炸弹进行 bfs 获得金币。
考虑 $S = 12$:我不知道我在哪里。但是我知道我现在可能在的位置集合!设 $f _ {i, j, U}$ 表示在 $(i, j)$,可能的起点位置集合是 $U$,所能拿到的最大金币数量。转移则只走必然安全的位置。剪剪枝随便过。
虽然我也不懂为什么但是胡出来 $S = 12$ 没胡出来正解。
正解大概是,发现原来有一个可能的起点集合 $U$,那么它会带来一些安全位置,这些位置全走一遍是不亏的,因此全走一遍,之后发现 $U$ 可能就缩小成了 $U'$,带来了新的安全位置。没缩小就没法走了,直接退出。之后不断搜索,直到没有缩小。
朴素实现复杂度好像是 $O(NMS^2)$ 的,不过 bitset 随便压一下就能除以一个 $w$(可以直接对 $S$ 压位,就是 $O(NMS)$ 的了)。
ABC077D Small Multiple
Statement
给定一个整数 $K$。求一个 $K$ 的正整数倍 $S$,使得 $S$ 的数位累加和最小。
$2 \le K \le {10}^5$,$K$ 是整数。
Solution
Solution
考虑找到一个按照数位和从小到大搜索正整数的过程:从 $1$ 开始,每次可以乘十或者加一(可以忽略进位的影响,因为数位和会被计算的偏大)。于是,只需要留存在模 $K$ 后为某个数时数位和最小的那个正整数即可。做一个 01bfs,乘十的边权为 $0$,加一的边权为 $1$,最后答案就是从 $1$ 到 $0$ 的最短路。
GYM105310I Vines
Statement
维护一个长为 $n$ 的序列 $a _ {0, 1, \ldots, n - 1}$,最初都为 $0$。有 $q$ 次操作,每次操作有三种:
- 给定 $i$,令 $a _ i = 1$;
- 给定 $k$,对所有 $i \bmod c \equiv k$ 的 $i$,令 $a _ i \gets a _ i + 1$;其中 $c$ 是一个初始时给定的常数;
- 给定 $i$,不断令 $i \gets \min(n, i + a _ i)$(认为 $a _ n = 0$),求最后会停在哪里。
$1 \le n, q \le 10 ^ 5$,$1 \le c \le n$。
Solution
Hint 1
考虑 $c = n$ 的情况。
Solution
如果 $c = n$,那么就是单点加,可以考虑一个分块算法(LCT 也可以,不过相当复杂而且常数巨大,所有不考虑):令块长为 $B$,那么每 $B$ 个元素作为一块,维护它们向后跳到块外的位置(或者就在块内停下),这样每次修改就暴力重构该块,查询可以快速跳跃,复杂度 $O(n + q(B + \frac{n}{B}))$。
对于一般的 $c$,首先可以快速维护 $a _ i$。当某次修改时 $a _ i + i$ 已经跳出块时,就不必再重构这个块了,否则暴力重构。这样,对于所有点,重构次数最多是 $O(B(n+q))$ 的(初始时每个点 $B$ 次,操作 $1$ 会使每个点多 $B$ 次),于是总复杂度就是 $O(\frac{nq}{B} + B^2(n+q))$,平衡一下就是 $O((n+q)^{5/3})$ 的。
多树
Statement
给定 $n, k$ 和 $k$ 棵有 $n$ 个点的树。对于每个点对 $(i, j)$,求出其在每棵树上的路径经过的点(含端点)的交集大小。
$1 \le n, k \le 500$。
Solution
Hint 1
对于某一棵树,考虑 $x$ 在 $(u, v)$ 路径上的充要条件:$dis(u, x) + dis(x, v) = dis(u, v)$。
Hint 2
无论 $x$ 是哪个点,都有 $dis(u, x) + dis(x, v) \ge dis(u, v)$。
Solution
所以可以直接对所有树的 $dis(x, y)$ 求和,记为 $d(x, y)$。
那么 $x$ 在一直 $(u, v)$ 路径上的充要条件就是 $d(u, x) + d(x, v) = d(u, v)$。一旦有某棵树不在其路径上,那么就不会相等。
然后直接三次方求距离和枚举点对即可。
NOISG 2021 E pond
Statement
(注:该题面和原题面对事物的称呼不同)
在数轴上种植着 $n$ 棵树。树被编号为 $1, 2, \cdots, n$。其中对于每个 $1 \le i \le n - 1$,第 $i$ 棵树与第 $i + 1$ 棵树之间的距离为 $x_i$。
初始时,你站在第 $m$ 棵树所在的位置上,所有树的高度均为 $0$。随后,在每单位时间,每一棵树均会增加 $1$ 单位的高度。
当你站在某棵树所在的位置上时,你可以不花费任何时间将其砍伐。当一棵树被砍伐后,它便会死亡,在接下来的时间不再生长。同时,你也可以花费 1 单位的时间,从当前的位置向左或向右移动 1 单位的距离。
你的任务是砍伐所有的树木。但是由于砍伐树木非常消耗你的精力,因此你希望你砍伐所有树木的高度之和最小。你想要知道,在最优的策略下,你所砍伐的树木的高度之和是多少。
$2 \le n \le 3 \times 10 ^ 5$,$1 \le m \le n$,$1 \le x _ i \le 10 ^ 6$。
Solution
Solution
设树 $i$ 的位置是 $s _ i$。设在某个(经过的树的集合,当前位置 $p$,当前时间 $t$)的状态下,若树 $i$ 没被走过,则 $C _ {i} = |s _ i - p| + t$;否则 $C _ i$ 是 $i$ 被走到的时间。设 $w$ 表示所有树的 $C$ 的和。那么,走过所有树时,$w$ 即为答案。发现 $w$ 随时间不减。其实走到 $1$ 或 $n$ 时 $w$ 就是答案了。
这其实是贡献提前处理的思路。
设 $f _ i$ 为走到 $i$ 时 $w$ 的最小值。设 $i \le m$,$j \ge m$,那么 $f _ i$ 到 $f _ j$ 的转移是 $f _ i + 2(i - 1)(s _ j - s _ i) \to f _ j$。像一个最短路一样,类似最短路的跑 dp。
显然 $f$ 值有单调性,$m$ 处最小而越远越大。维护当前已确定的部分(是个区间),斜率优化计算左端点减一和右端点加一处的可能的 $f$,取较小值加入已确定的部分。重复直到完成。
GCJ 2009 Final C Doubly-sorted Grid
Statement
给定一个 $n \times m$ 的矩阵,有些地方填了小写字母,有些地方没填。求填满小写字母后,要求每行每列都递增时的方案数。
$1 \le n, m \le 10$。
Solution
Hint 1
每行每列都递增,那么所有小于等于某个字符的所有字符组成了左下角到右上角的一条路径。
Solution
请先看 Hint 1。
设 $f _ {i, P}$ 表示填完了前 $i$ 种字符,其状态(路径)为 $P$ 的方案数。
转移就是从 $f _ {i - 1}$ 转移到 $f _ i$,这是一个类似前缀和的操作,即对于每条路径要求出完全在其左上角的路径的 $f$ 值的和。随后需要删除一些不合法的状态,这个是容易做的。
前缀和操作比较困难。有一个容斥做法:先令 $f _ {i, P} \gets f _ {i - 1, P}$。考虑某条路径 $S$ 里所有向右一次再向上一次的子路径,可以考虑把它变成向上再向右(就是删去了这个凸出部分的格子)之后的一条新路径 $P'$,然后让 $f _ {i, P} \gets f _ {i, P} + f _ {i, P'}$。但是这样会算重复,因此考虑要求所有左上方路径系数都为 $1$ 时应当如何分配系数。可以发现,直接枚举凸出部分格子的子集 $R$,然后 $f _ {i, S - R}$ 的系数就是 $(-1) ^ {|R| - 1}$。无论左上方路径和 $P$ 的重合的突出格子数量有多少个,都能得到其系数为 $1$。
这样做经过卡常可以通过 QOJ 数据,但是并非最优解,复杂度也并不优(或者说根本没法算真实复杂度)。
有一个更快速的做法。令 $g _ {i, P, j}$ 表示填完了前 $i$ 种字符,当前路径为 $P$,前 $j$ 个突出格子都突出的所有路径的和。$g$ 的转移就按 $j$ 从大到小转移,考虑第 $j$ 个格子 $o$,那么 $g _ {i, P, j - 1} = g _ {i, P - o, j - 1} + g _ {i, P, j}$。那么复杂度就是 $O(\binom{n+m}{n}\times (n+m) \times |\Sigma|)$ 的。
代码实现。我常数比较大,所以跑的也不太快。
LOJ6897 约树
Statement
给定正整数 $n\ (n \ge 3)$,你需要构造一棵 $n$ 个节点的树,点有点权,使之满足如下要求。
- 对于任一节点,其点权为不超过 $11000$ 的正整数。
- 对于任一不大于 $n$ 的正整数 $k$,都存在树上的一条长度不小于 $1$ 的链,使得该链上所有点权的最大公约数为 $k$,其中链的长度定义为其经过的边数。
在本题的数据范围内答案一定存在,如果有多种构造方案,输出任意一组即可。
$n \le 2500$。
Solution
Solution
当之无愧的神仙 Ad-hoc 题。涩爆了
出题人阚神原做法是随机构造菊花图的拼接,很难写而且不优美,证明办法是遍历所有可能的 $n$ 然后发现都能跑出解(x)。
更优的解法是 myee 老师提出的,参考 社论。
考虑所有质因子只有 $2, 3$ 的数。如果想让它们都出现,可以按照以下方式构造一条链:
1 2 4 8 16 (32)
3 6 12 24 (48)
9 18 (36) (72)
27 (54)
(81)将数字按照以上方式排列,然后把这样的表格的最外面一圈连起来,比如这个例子就是 $81 \to 54 \to 36 \to 72 \to 48 \to 32$。此时,表格内任意一个数字都可以被这条链上的某个区间得到。
于是有一个朴素的想法:找到所有不含质因数 $2, 3$ 的数 $x$,并按照以上方式排列所有形如 $2 ^ a 3 ^ b x$ 的数,然后把链拼起来。尝试计算一下这种构造方式的消耗:最大值显然不会超过 $3n$,链长度则是下面这个式子:
$$ \sum \limits _{2\nmid z, 3 \nmid z}^{n} \left(\left\lfloor \log_2 \left( \left\lfloor\frac{n}{z}\right\rfloor \right) \right\rfloor + 2\right) $$
注意到 $\sum \limits _{2\nmid z, 3 \nmid z}^{n} \left(\left\lfloor \log_2 \left( \left\lfloor\frac{n}{z}\right\rfloor \right) \right\rfloor + 1\right)$ 就是上面表格里第一行数字的个数,也就是所有不是 $3$ 的倍数的数的个数,也就是 $n - \left\lfloor\frac{n}{3}\right\rfloor$。
另外的部分,就是 $\sum \limits _{2\nmid z, 3 \nmid z}^{n} 1$,也就是不含质因数 $2, 3$ 的数的个数,可以发现 $n$ 每增大 $6$ 时它是有循环节的,手摸一下可以得到当 $n \equiv 1, 2, 5 \pmod 6$ 时,其值为 $\left\lfloor\frac{n}{3}\right\rfloor + 1$,否则为 $\left\lfloor\frac{n}{3}\right\rfloor$。
于是,某些时候构造出的链会长一点。在 $n$ 比较大的时候,可以取两个大于 $\frac{n}{2}$ 的数,然后用三个数把它们连起来,这样就节省了一格长度。随便取一对 $\operatorname{lcm}$ 比较小的数就可以了。
不过,在 $n = 5$ 时没法这么干,特判一下。
这样构造的最大值在 $n$ 足够大时,可以取一个 $w$ 使得 $5w > \frac{n}{2}$ 且 $w$ 尽量小(也就是说 $5w = \frac{n}{2} + O(1)$,然后把 $5w$ 和 $7w$ 连起来,这样最大值就是 $\operatorname{lcm}(5w, 7w) = 35w = 3.5n + O(1)$。
LOJ6878 生不逢时
Statement
给定正整数 $n, m$ 和 $n$ 个区间,第 $i$ 个区间为 $[l _ i, r _ i]$,保证 $0 \leq l_i \leq r_i < 2^m$。
对于非负整数 $x$,记 $S _ m(x)$ 表示 $x$ 在二进制下最低的 $m$ 位依次连接成的 01 串,如果不足 $m$ 位则在高位补 $\texttt 0$。
对于 $k = 1, 2, \cdots ,n$,求有多少非负整数序列 $a _ 1, a _ 2, \cdots, a _ k$ 满足下列条件。
- 对于所有 $1 \leq i \leq k,l _ i \leq a _ i \leq r _ i$。
- $S _ m(a _ 1 \oplus a _ 2 \oplus \cdots \oplus a _ k)$ 是回文串,其中 $\oplus$ 表示按位异或运算。
答案对 $998244353$ 取模。
$1 \le n \le 40$,$1 \le m \le 60$,3s,2G。
Solution
Hint 1
异或后是回文串,等价于每个数对折之后异或后是 $0$。
Hint 2
考虑一个对 $2^m$ 开的线段树结构。以下的“线段树区间”均指这个线段树的某个结点的区间,即 $[p, p + 2 ^ k)$(其中 $2^k \mid p$)。称区间 $[0, 2 ^ {\lfloor \frac{m}{2} \rfloor})$ 为满半区间。
对于每个原先的区间,将其拆成线段树区间后,对于每个线段树区间,将其每个数对折之后,其仍然是一个线段树区间,不过会带系数。
证明可以分类讨论该线段树区间长度有没有超过 $2 ^ {\lfloor \frac{m}{2} \rfloor}$。超过了就是满半区间,没超过就是一个小区间。
Hint 3
其本质是异或卷积,最后只求 $0$ 的值,于是可以考虑 meet-in-the-middle,分成两半求出来之后再对位拼起来。
Hint 4
考虑两个线段树区间,要求两个区间的每个位置分别带相同的系数(区间内部一样,两个区间可以不同)的异或卷积,其还是一个带相同系数线段树区间。考虑区间的长度,结果的区间长度是较长区间的长度,每个位置的系数是两个区间的系数乘起来再乘短区间长度。
Hint 5
将区间 $[0, r _ i)$ 对折后,可以写成一些满半区间和一个不到满半区间的前缀其中每个数异或上某个数的结构。
将区间 $[l _ i, r _ i]$ 对折的话,就可以做差分,和上面是一样的。
Hint 6
考虑维护一个对 $2 ^ {\lfloor \frac{m}{2} \rfloor}$ 开的线段树,如果某个区间内数字全部相同就在这个区间停下,不再向下开结点。
Solution
题外话:为什么 kan 是神?
这道题的 idea 来源是联考有一个一堆区间做异或卷积的题,但是阚神写出了这个超厉害的数据结构,经过讨论后发现可以加强(原来是 $O(m2^n)$ 求单点值),然后又决定套个壳子,我提了说回文是不是可以套!然后阚研究了一下发现真可以,于是就出出来了。其实这有点像线段树的“乘法”(当然这个概念并没有定义,只是看着像而已)。
这个题原先的名称是遥不可及,和之前那个题“约树”被出在了一场 noip 模拟赛里,约树是 t3,这个题是 t4。约树只有 myee 老师通过,这道题无人通过,其难度由此可见一斑。
这个数据结构是线段树和 01 trie 的结合体,加上这个神秘的操作,于是我们称之为 KKT(Kan Kami Tree),阚神树!
请先按顺序看完所有 Hint。
接下来的问题是如何做一个线段树和一个前缀异或上某个数的异或卷积。其应当也能表示成一个线段树。
设计函数 solve(&nrt, rt, R, xr, coef, r),其中 nrt 为新树结点指针,rt 为旧树的,r 为当前区间长度,R 和 xr 分别表示前缀长度和异或值,coef 表示前缀的系数。
实际上,新树、当前树和要卷积的前缀在真实位置上并不是对齐的,这是由于异或卷积的特性导致的。我们想要把这个“对齐”操作放在调用函数之前做。于是就只需要关心当前区间长度了。
首先,如果当前树为空,返回。
如果前缀是满的,那么直接更新新树当前结点的信息,其每个位置会加上旧树当前区间内所有数的和再乘上系数 coef。由此,我们可以看出需要维护的信息至少有区间和。
令 $2 ^ k = r$,我们想要去掉异或前缀的位置的影响:如果 xr 的第 $k - 1$ 为 $1$,那么以下操作都可以直接交换旧树的左右孩子来看待。对前缀异或等价于对旧树异或。于是就转化成了真实前缀(虽然 xr 更低的位也会有值,但是这和当前位置是无关的)。
- 如果前缀长度短于区间一半,那么结果就是新树左侧加等于旧树左侧卷积前缀,右侧也一样。
- 否则,想像一下异或卷积,就会有两个满的部分,这和上面是一样的。对于不满的部分就是新树左侧加等于旧树右侧卷积上前缀的右半部分,新树右侧加等于旧树左侧卷积上前缀的右半部分。
于是递归做就可以。
在维护区间和,合并两个孩子的时候,不能直接合并(要不然满前缀的区间加没法做),需要再维护一个区间加的 tag,应该只能标记永久化。需要注意,在卷积前缀的 pushup 时,需要用旧树的 tag 更新一下新树的 tag。
卷积前缀后,需要把两次卷积前缀的结果加起来,可以直接做在同一棵树上从而省去了合并的过程。
接下来还有一个问题,就是如何得到两个线段树(称为 A 树和 B 树)的对位乘积。有个很暴力的做法是暴力递归,直到 A 树和 B 树都没有当前结点,此时计算一路上的 tag 之和的乘积。复杂度没问题,但是常数大,会被卡常一个点。
关于为什么不能下传区间加标记也在这里:下传之后会让两棵树大小相同,从而结点数变大变高,复杂度就错了。可以看最后的复杂度证明。
另一个做法是类似线段树合并的,只有两个线段树都有的结点才会遍历到,在每个点上算贡献。
$$ \begin{align*} &\sum a _ i b _ i \\ =&\sum (a _ i' + tag _ a)(b _ i' + tag _ b) \\ =&(\sum a _ i'b _ i') + tag _ a(\sum b _ i) + tag _ b(\sum a _ i) - len \times tag _ a \times tag _ b \end{align*} $$
按照上式算即可。
接下来是复杂度证明。
首先,复杂度等于两树的总结点数之和。如果某个结点有一个孩子,把它另一个孩子也建出来,这样和原来的复杂度显然一样。
考虑卷积前缀的过程,可以发现如果这样建了孩子,那么每个旧树结点恰好得到一个新树结点。之后再合并两次卷积的结果,所以结点数最多会乘以 $2$。初始时需要给位置零加一,是 $m$ 个结点。于是合并 $n$ 个区间后结点数就是 $O(m2 ^ n)$ 的。这个东西做一次前缀和还是自己,再算上 meet-in-the-middle,总时空复杂度就是 $O(m 2 ^ {n/2})$。
常数不小也不算大(因为结点很多时候是重合的),实现优秀可以跑很快。
代码可以直接在 loj 上看。

题目确实够涩,爱了/se