10circle 算法学习笔记

实际上……还有很多没补的。以后会补的（确信（
也会有一些技巧之类的。

可能需要一些 OI 基础。
不保证看完就能明白，但是会尽力让人能看明白的。

最近更新：分拆成了一些小项。
分拆中，此页面仅作汇总。

平衡树-Treap 及其拓展
数据结构是好的。平衡树一篇就已经巨长所以单独拆出来。
分治宣讲
一个讲稿，感觉挺好的就放博客上来。
[树形数据结构及拓展]()
数据结构是好的。树形也不只是树。含线段树、左偏树、可持久化数据结构、ST 表、树状数组、KDTree、李超树。
[图论算法]()
含欧拉回路、欧拉路径、Tarjan 算法、拓扑排序、网络流算法、有向图最小生成树（最小树形图）、次小生成树、k 短路和图匹配算法。
[经典图论模型与图的性质]()
如题，含 2-SAT、差分约束、二分图的各个结论、网络流经典建图和最大流最小割定理。
[OI 中的字符串算法及自动机]()
有各种字符串算法和自动机相关题目，含有 Hash、Trie 树、AC 自动机、后缀数组、后缀自动机、回文自动机、kmp、exkmp（Z 函数）、Manacher 和自动机上 dp。
[组合数学]()
含容斥原理、各种数、Lucas 定理、各种组合等式、生成函数、形式幂级数和例题。
[线性代数]()
含向量、矩阵基础、矩阵快速幂、高斯消元、行列式和二维向量的各种运算和用处，大概也算是二维计算几何基础。
[OI 中组合数学常见知识]()
含矩阵树定理、Prufer 序列、LGV 引理。
[树的性质及树相关算法]()
含树上启发式合并、点分治、括号序列和树的关系、树链剖分、Euler Tour Tree。
[群论基础和群在计数中的应用]()
群是好的，群在旋转而又跳跃。
[数论基础]()
含数论函数简介、狄利克雷卷积、莫比乌斯反演和原根。建议和群论基础一起读。
[数论算法]()
含线性筛、线性基、中国剩余定理、数论分块、BSGS、欧几里德算法（gcd 和 exgcd）。
[复杂 dp 及优化]()
含斜率优化（凸包/李超树）、四边形不等式、数据结构优化 dp、插头 dp 等。
[多项式及其算法]()
含拉格朗日插值、FFT & NTT 等。
[杂项和技巧]()
含 set 维护颜色连续段、WQS 二分、分数规划、莫队、CDQ 分治、整体二分、分块、根号分治、打表、找规律、扫描线、表达式求值、搜索和随机算法等。
[博弈论]()
[二维计算几何]()
含凸包、旋转卡壳、半平面交等。

原先的内容见下。

实际上……还有很多没补的。以后会补的（确信（
也会有一些技巧之类的。
由于太长了，加载太慢，准备分拆。
正在改版中……应该很快就能更新出来。
最近更新：更新了拓展欧几里德算法。

WQS 二分

树上启发式合并（DSU on Tree）

CF1009F

欧拉回路

连通性问题

2-SAT

网络流

二分图模型

KMP

拓展 KMP

AC 自动机

JUMP JUMP！！

这个东西是用来解决一堆字符串共同执行某个操作的（比如查询在另一个字符串中出现的次数）。

首先对这一堆字符串建一个字典树。字典树上一个节点就是一个状态，可以表示从根到它的边所连起来形成的字符串，即某个（些）串的一个前缀。下文 $u$ 均表示某个状态。定义 $\texttt{fa}_ u$ 为 $u$ 在字典树上的父亲状态，$\texttt{to}_ {u,c}$ 为 $u$ 状态再接 $c$ 后的状态。

AC 自动机中最重要的就是 $\texttt{fail}$ 指针了。$\texttt{fail}_ u$ 就指向 $u$ 所表示的字符串在本字典树内的最长后缀的状态。感觉自己不会说话，如果不明白可以看 OI-wiki 中对 $\texttt{fail}$ 指针的说明。

构建 $\texttt{fail}$ 指针需要从短到长构建。

若 $\texttt{to}_ {\texttt{fail}_ u,c}$ 存在，则 $\texttt{fail}_ {\texttt{to}_ {u,c}}=\texttt{to}_ {\texttt{fail}_ u,c}$，即本字符串与最长后缀同时增加了字符 $c$，显然还是最长后缀。

其余情况，需要不断向前跳。由最长后缀跳到最长后缀的最长后缀……直到存在 $c$ 的边。这样可以从长到短遍历所有在字典树中的本字符串的后缀。如果始终没有 $c$ 的边，则 $\texttt{fail}_ u$ 就是空串。

但是这样不好写而且慢，需要优化。跳，可以路径压缩。因为不存在 $\texttt{to}_ {\texttt{fail}_ u,c}$，所以可以把它设成跳完的，即 $\texttt{to}_ {\texttt{fail}_ {\texttt{fail}_ u},c}$，相当于直接扯到存在 $c$ 的地方了。

查询就沿字典树游走。由于已经进行了路径压缩，不用判断到结尾要跳 $\texttt{fail}$。沿 $\texttt{fail}$ 累加某个状态出现了多少次。就是先枚举子串后端点，再沿 $\texttt{fail}$ 跳前端点。但是这样不好，慢。需要先标记一下，最后再累加。这样就是线性的了。

Code

Build fail: 
queue<int>q;
for(int i=0;i<26;i++)if(tr[0][i])q.push(tr[0][i]);
while(!q.empty()){
    int u=q.front();q.pop();
    for(int i=0;i<26;i++){
        if(tr[u][i])f[tr[u][i]]=tr[f[u]][i],q.push(tr[u][i]);
        else tr[u][i]=tr[f[u]][i];
    }
}

query:
int u=0;
for(int i=0;s[i];i++){
    u=tr[u][s[i]-'a'];
    ct[u]++;
}

例题：洛谷的板子、[BJOI2017] 魔法咒语（矩阵快速幂、自动机上 dp）、[JSOI2007] 文本生成器（自动机上 dp）

后缀数组

后缀自动机

组合数学

卡特兰数及应用

插板法

容斥

线性代数

依铃也不知道为啥叫“线性代数”……反正是这个名（

向量

这里面首先有“向量”这个概念。既有大小又有方向的量称为向量。但是在 OI 中除了 FFT 好像都可以只用坐标表示向量。向量记作 $\vec{a}$ 或 $\mathbf{a}$。

比如一个二维向量，就可以表示为 $(a,b)$ 的样子。就相当于变化量。当然向量也有多维的，于是 vector 就出现了。一个 $n$ 维的向量可以用 $(a_1,a_2,\cdots,a_n)$ 表示。用坐标理解这个东西可能好理解些。零向量没有大小，自然也不确定方向，相当于一个点，用 $\mathbf{0}$ 表示，其 $n$ 维坐标都是 $0$。

向量是可以相加的，变化量可以在这里体现。比如 $\mathbf{a+b}=(a_1+b_1,a_2+b_2,\cdots,a_n+b_n)$，就是每一维相加。相减类似，也是每一维相减，可以理解为 $\mathbf{a+(-b)}$。加的几何意义就是从原点开始按照 $\mathbf{a}$ 平移之后再按照 $\mathbf{b}$ 平移。比如一个点 $(x,y)$ 按二维向量 $(a_1,a_2)$ 平移后就会变成 $(x+a_1,y+a_2)$。这个东西可能有图更好理解些……但不好弄（。可以自己画几个图感受一下（，依铃不太会说（。不过这东西高中会学的。

向量还可以数乘，就是直接放大一些倍。$k\mathbf{a}=(ka_1,ka_2,\cdots,ka_n)$，然后方向就可能相反，也可能和原来一样。

两个向量共线就是说这两个线段平行（向量是可以任意平移的，就和线段一样，端点变了但是大小方向不变也是同一个向量），用数乘表示就是两个非零向量 $\mathbf{a}$ 与 $\mathbf{b}$ 共线 $\iff$ 有唯一实数 $k$，使得 $k\mathbf{a}=\mathbf{b}$。

向量的模就是向量的长度也就是向量的大小（明明是一个东西但它就是有一堆词），用 $|\mathbf{a}|$ 表示。$|\mathbf{a}|= \sqrt{a_1^2+a_2^2+\cdots+a_n^2}$。（这就是两点间距离公式，应该还好，会勾股定理就能推出来）。

矩阵及快速幂矩阵的设计

还有一个东西，叫矩阵。

$$\begin{bmatrix}a_{1,1}&\cdots&a_{1,m}\\\vdots&\ddots&\vdots\\a_{n,1}&\cdots&a_{n,m}\end{bmatrix}$$

这是一个 $n$ 行 $m$ 列的矩阵，你可以当它是一个二维数组。这里依铃用 $A_n$ 表示 $A$ 的行数，$A_m$ 表示 $A$ 的列数，$A_{i,j}$ 表示 $A$ 中第 $i$ 行第 $j$ 列的元素。

矩阵的加减要求 $A_n=B_n,A_m=B_m$，即运算的两个矩阵行数和列数相等，然后逐个元素进行。

矩阵的乘法要求 $A_m=B_n$，即第一个矩阵的列数等于第二个矩阵的行数。然后，设结果为 $C$，那么 $C_{i,j}=\sum_{k=1}^{A_m}A_{i,k}B_{k,j}$。显然 $C_n=A_n,C_m=B_m$。通俗的讲，在矩阵乘法中，$C$ 矩阵的第 $i$ 行第 $j$ 列的数，就是由 $A$ 第 $i$ 行的 $A_m$ 个数与 $B$ 第 $j$ 列的 $A_m$ 个数分别相乘再相加得到的。矩阵乘法没有交换律，但满足结合律。

接下来是用处，矩阵加速递推。有一个递推式，其中 $k_i$ 给定：

$$\large{f_i=k_1f_{i-2}+ k_2g_{i-1}+k_3f_{i-1},\ \ g_{i}=k_4g_{i-2}+k_5g_{i-1}+k_6f_{i-2}}$$

于是思考将它优化至 $\mathrm{O}(\log n)$，这需要构造一个初始矩阵 $A_2$ 和一个转移矩阵 $B$。$A_i$ 需要包含 $f_i,f_{i-1},g_{i},g_{i-1}$，可以写做 $$\begin{bmatrix}f_i&f_{i-1}&g_i&g_{i-1}\end{bmatrix}$$。而 $B$ 需要将 $A_{i-1}$ 转移到 $A_i$，可以写做：

$$\begin{bmatrix}k_3&1&0&0\\k_1&0&k_6&0\\k_2&0&k_5&1\\0&0&k_4&0\end{bmatrix}$$

然后答案矩阵为 $A_2B^{n-2}$。它可以写作 $\begin{bmatrix}f_n&f_{n-1}&g_n&g_{n-1}\end{bmatrix}$。注意可以优化的递推式只有常系数（好像是的）。快速构造的方法就是

$$\begin{bmatrix}&f_i&f_{i-1}&g_i&g_{i-1}\\f_{i-1}&&&&\\f_{i-2}&&&&\\g_{i-1}&&&&\\g_{i-2}&&&&\end{bmatrix}$$

然后往里面填数就行。左侧就是矩阵乘法中那个 $A_{i-1}$，而转移后就是上面的一行，也就是要求的 $A_i$。然后快速幂就行。

矩阵也可以表示变换，方式同上，不细说了。

例题：Luogu 板子、[NOI2011] 兔农，[NOI2021] 密码箱（还用平衡树）。好了差不多讲完了，可以写题了（？。

模板代码

struct matrix{//为方便起见，程序中下标从 0 开始。
    ll a[N][N];
    matrix(int ag=0){
        memset(a,0,sizeof a);
        if(ag)for(int i=0;i<N;i++)a[i][i]=1;
    }
};
matrix operator*(const matrix &a, const matrix &b){//由于内存不连续访问常数较大
    matrix c;
    for(int i=0;i<N;i++){
        for(int j=0;j<N;j++){
            for(int k=0;k<N;k++){
                c.a[i][j]=(c.a[i][j]+a.a[i][k]*b[k][j])%mod;
            }
        }
    }
    return c;
}
/*matrix operator*(const matrix &a, const matrix &b){//常数较小
    //自己思考x((
}*/
matrix pw(matrix a, ll k){
    matrix ans(1);
    while(k){
        if(k&1)ans=ans*a;
        a=a*a;k>>=1;
    }
    return ans;
}

分数规划

高斯消元

中国剩余定理

拉格朗日插值

大纲里没有但是它考了。离谱。

莫比乌斯反演应用

数论分块

群及其应用

进行运算的东西和结果的类型相同（类型的概念很模糊，只是为了感性理解。如果是群或类似概念，就是在一个集合中）的运算是有封闭性的。比如 $<$ 在实数范围内就是没有封闭性的。

为了更好的探究运算的性质，数学家们引入了群。群由一个集合和一个集合上的运算构成。如果二元运算 $\cdot$（泛指运算）在集合 $G$ 中有封闭性和结合律（注意并不用交换律），那么它们就构成了半群 $(G,\cdot)$。注意这还不是群，只是半群。

群还需要单位元。单位元一般用 $e$ 表示。它的定义是 $\forall a \in G, e\cdot a= a\cdot e = a$。$\forall$ 的意思就如同它的 LaTeX 名一般，是“对于所有”的意思。$\in$ 的意思也如同它的 LaTeX 名一般，是表示一个元素属于一个集合的意思。为啥叫单位元呢，首先这是个元素，而且它就像是单位 $1$ 一样，任何数和它做运算都不会改变。含有单位元的半群叫做含幺半群。

思考 1：会不会存在两个单位元呢？可以试着写出证明。tip：$e_1 \cdot e_2=?$。既是 $e_1$ 又是 $e_2$，所以只有一个单位元。

思考 2：若 $\forall a \in G, e_l\cdot a = a$，$\forall a \in G, a\cdot e_r = a$，那么 $e_l$ 和 $e_r$ 是不是相同呢？

证：$$\because \forall a \in G,e_l \cdot a = a\ \ \ \ \therefore e_l\cdot e_r=e_r$$ （第一步,就是说把 $a$ 替换为 $e_r$ ）

$$\because \forall a \in G,a\cdot e_r = a,\ \ \ \ \therefore e_l\cdot e_r=e_l$$ （第二步）

$$ \therefore e_l\cdot e_r=e_l=e_r$$ （第三步）（非常简单是不是（

也许需要举个例子……？比如 $(\Z,+)$ 就是一个含幺半群（也是一个群），其中 $\Z$ 指整数集。对，单位元 $e=0$。但是 $(\Z,\times)$ 是含幺半群却不是群，因为逆元（下面讲）可能不是整数，不属于整数集合 $\Z$。

然而含幺半群还不是群，群中的每一个元素还有它的逆元。$a$ 的逆元一般用 $a^{-1}$ 表示。同时，在下面的叙述中，$a^{-1}$ 都指逆元。逆元的定义是 $a^{-1}\cdot a = a\cdot a^{-1}=e$。注意，下面两个都是在含幺半群的条件下的证明，不是所有元素都有逆元。

思考 3：逆元可能有两个吗？

思考 4：若 $a^{-1}_l \cdot a =e, a\cdot a^{-1}_r=e$，那么 $a^{-1}_l$ 和 $a^{-1}_r$ 是否相同？（显然下面这个问题严格强于上面的，因此只证下面的了。

证：$\because a^{-1}_l \cdot a =e,\ \ \ \ \therefore a^{-1}_l \cdot a \cdot a^{-1}_r=e\cdot a^{-1}_r=a^{-1}_r$。

$$\therefore a^{-1}_l \cdot (a \cdot a^{-1}_r)=a^{-1}_r,\ \ \ \ \therefore a^{-1}_l \cdot e=a^{-1}_r,\ \ \ \ \therefore a^{-1}_l=a^{-1}_r $$

群要求 $\forall a \in G, \exist a^{-1},\text{ s.t. }a^{-1}\cdot a = a\cdot a^{-1}=e$。$\exist$ 的意思就和它的 LaTeX 名一样，是“存在一个”的意思。$\text{s.t.}$ 全称 subject to，意思是使得…满足…。于是群的定义就讲完了。

群中一个元素和它自己做 $k$ 次运算，即 $$\begin{matrix}\underbrace{a\cdot a \cdots a}\\k\end{matrix}$$，表示为 $a^k$。看着和幂很像，也可以以幂理解，但不一样。那么，很显然的，这个有整数幂的性质，包括负数。

比如一个长度为 $n$ 的排列（置换）和上面所说的运算就是一个群，易证。

乘法逆元也是在一个群中的逆元。这个群是 $(\Z^{*}_{n},\cdot)$。其中 $\Z^{*}_{n}=\{i|1\le i \le n,(n,i)=1\}$，也就是说在 $[1,n]$ 中与 $n$ 互质（$(a,b)$ 可以表示 $a,b$ 的最大公约数）的正整数组成的集合。而 $\cdot$ 是指在 $\bmod n$ 意义下的乘法。封闭性比较显然吧，从质因数的角度分析。

思考5：它为什么所有元素都有逆元？

证：首先转化问题为 $(a,n)=1\Leftrightarrow \exist x \text{ s.t. } a\cdot x \equiv1\pmod{n}$（$a$ 和 $x$ 均为小于等于 $n$ 的正整数）。就是说，$a$ 与 $n$ 互质等价于存在一个 $x$ 使得 $a\cdot x$ 在 $\bmod n$ 的情况下和 $1$ 相等，也就是和 $e$ 相等。

算了这个太难打完了就不打了吧（

来源：《应用近世代数》清华大学出版社胡冠章王殿军编著

应用以后再写（

数论函数简介及其性质与算法

积性函数

狄利克雷卷积

BSGS 及其拓展

注：此节内所有变量所表示的数均为非负整数。

基础 BSGS

基础 BSGS 算法可以在 $O(\sqrt{p})$ 或 $O(\sqrt{p}\log{p})$ 的时间内，$O(\sqrt{p})$ 的空间内解决已知 $a,b,p\ (\gcd(a,p)=1)$，求最小非负整数 $x$ 使 $a^x\equiv b \pmod p$ 的问题。

设 $k=\lceil\sqrt{p}\rceil$。由原式两侧同乘 $a^r$，其中 $r$ 为满足 $1\le r \le k$ 且 $k|(x+r)$ 的最大值，可得 $a^{x+r}\equiv a^{r}b \pmod p$。这个式子在 $(a,p)=1$ 时与原式等价。推得 $a^{qk}\equiv a^{r}b \pmod p$，则 $x=qk-r$，$1\le q\le k$。由 $a^{\phi(p)}\equiv 1 \pmod p$ 得出如果存在 $x$，则一定存在 $r,q$。

于是就可以先计算出 $ab$ 至 $a^kb$，并将它们放入 Hash 表或 STL map 中，值为 $a$ 的次方。注意如果 $a^db=a^eb\ (d<e)$，则表中这一项的值应为 $e$。

之后再从 $1$ 到 $k$ 枚举 $q$，推出 $a^{qk}$，并查表。如果查到，那么直接得出答案。如果枚举完还没查到，那么无解。

例题：[SDOI2011] 计算器、[SDOI2013] 随机数生成器。在这两题中，注意特判 $a=0$。

模板代码

typedef long long ll;
ll BSGS(ll a, ll b, ll p) {
    a %= p, b %= p;
    if(a == 0) return b? -1: 1;//0^0 未定义, 0^1=0 
    map<ll, int> mp;
    ll k = sqrt(p) + 1, c = 1; //k 再大些也无关紧要
    for(int x = 1; x <= k; x++) {
        c = c * a % p;
        mp[c * b % p] = x;
    }
    ll d = c;
    for(int q = 1; q <= k; q++) {
        if(mp.find(d) != mp.end()) return k * q - mp[d];
        d = d * c % p;
    }
    return -1; 
}

拓展 1

显然，有时不会满足 $(a,p)=1$ 的条件。OI-wiki 写的很好，就不写了吧（

拓展 2

有时又要求 $x^a\equiv b\pmod p$。OI-wiki 写的也很好，也不写了吧（

例题：CodeForces 1106F（还用矩阵快速幂）

欧几里德算法及拓展欧几里德算法

大概这东西算是依铃学的最迷糊的比较简单的算法了……所以来补一补。（其实是做题遇到了发现就这算法不会（

欧几里德算法求 $\gcd$

欧几里德算法求 $\gcd$ 就是由于 $\gcd(a,b)=\gcd(a,a%b)$ （$b$ 不为 $0$ 时）、$\gcd(a,0)=a$，所以每次用较大的数模较小的数，至少减少一半，因此复杂度是 $\log$ 的。也叫辗转相除法。在 OI-Wiki 上有详细的讲解，就不说了吧（

扩展欧几里德算法求 $ax+by=\gcd(a,b)$ 整数解

而扩展欧几里德则使用了类似的辗转相除的方法来计算 $ax+by=\gcd(a,b)$ 的整数解。
设 $g=\gcd(a,b)$。

求解过程在 OI-Wiki 上写的很好，所以就不写了吧（

拓展欧几里德的应用

$ax+by=c$ 有整数解的条件

将 $ax+by=c$ 变换为 $g(\frac{a}{g}x+\frac{b}{g}y)=c$，显然 $ax+by=c$ 有整数解 $\Rightarrow$ $c=kg$（$k$ 是整数）

当 $c=kg$（$k$ 是整数）时，可通过以下方式求出解。
应用拓展欧几里得算法，求出 $ax+by=\gcd(a,b)$ 的一组解 $x^\prime,y^\prime$。再让 $x_0=kx^\prime,y_0=ky^\prime$，于是求得一组整数解 $x_0,y_0$。

因此 $ax+by=c$ 有整数解 $\iff$ $c=kg$（$k$ 是整数）

求出 $ax+by=c$ 的所有整数解

首先将 $a,b,c$ 都除掉 $g$ 使处理后的 $a,b$ 互质。

设 $x_0,y_0$ 为方程 $ax+by=c$ 的一组解。
$ax+by=a(x_0+bt)+b(y_0-at)=ax_0+abt+by_0-abt=ax_0+by_0=c$，所以，若 $x_0,y_0$ 为方程 $ax+by=c$ 的一组解，则该方程的解集为 $\{x,y|x=x_0+bt,y=y_0-at,t\in \R\}$。
当使用拓展欧几里德（以及上面的结论）求出一组整数解 $x_0,y_0$ 后，该方程的整数解集就是 $\{x,y|x=x_0+bt,y=y_0-at,t\in \Z\}$。

FFT & NTT

原根

计算几何基础

树链剖分

轻重链剖分

树链剖分，就是说把树拆成链来方便处理、维护。轻重链剖分，就是按照“轻重”孩子节点来剖分。考虑这么一道题（Luogu P3384）：

已知一棵包含 $n$ 个结点的有根树，每个节点上包含一个数值，需要支持以下操作：
1 x y z，表示将树从 $x$ 到 $y$ 结点最短路径上所有节点的值都加上 $z$。
2 x y，表示求树从 $x$ 到 $y$ 结点最短路径上所有节点的值之和。
3 x z，表示将以 $x$ 为根节点的子树内所有节点值都加上 $z$。
4 x，表示求以 $x$ 为根节点的子树内所有节点值之和。

某位神仙曾经说过，图上问题不会做，先考虑树怎么做。树上问题不会做，先考虑链上怎么做。
发现当树是链时，就是区间加区间查询和，用线段树维护即可。考虑把树变成一些链，使每个链上节点在重新标号后是连续的。这样就可以把一条路径拆成一些区间，并对每个区间分别加减。
显然分出来的链上节点只能有祖先孩子关系，就是说只能直上直下，不能在某个位置有从向上变成向下的转弯。否则就不能保证编号的连续。
对于某一个节点，它可以连上某一个孩子 $c_i$ 的链，而让其它孩子分别新建一个链。之后重编号时给自己编号后先给 $c_i$ 的这颗子树编号，就能保证编号连续。显然，$c_i$ 的选择直接影响到路径拆分出来的区间数，也就影响到了复杂度。

那么，$c_i$ 应该如何选择呢？
一种方式是发挥随机的精神，在所有孩子中随机选择 $c_i$。在数据随机时表现优秀，但是在极限数据下拆分出的区间个数是 $O(n)$ 的，如下图所示，从点 $1$ 到点 $n-1$ 的期望拆分出的区间个数约为 $\frac{n}{4}$。

随机选择的 hack

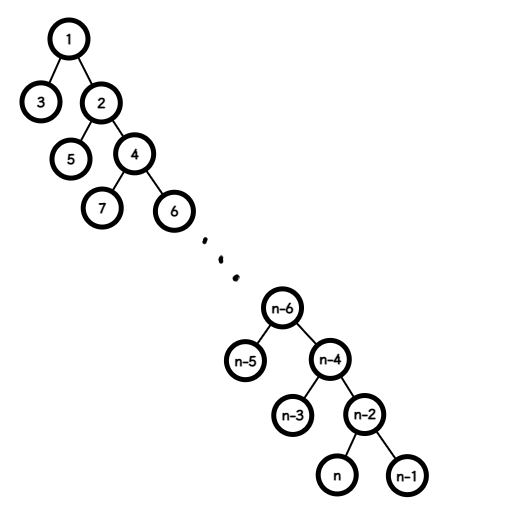
还有一种方式，考虑贪心。显然我们想使路径拆分出来的区间数最小，所以 $c_i$ 的子树最大会比较好。这就是重链剖分，可以证明拆分出的区间个数是 $O(\log n)$ 的。

（待补全）

长链剖分

长链剖分和轻重链剖分的用处差别比较大。

（待补全）

平衡树-Treap

平衡树分 leafy 和非 leafy。leafy 平衡树在叶子节点上存储原始信息，像线段树。非 leafy 则是每个节点上都有信息。实际上各种树型 $\log$ 之类的数据结构本质上都类似（比如平衡树、线段树、跳表），只是具体实现不同。

讲平衡树前，首先要讲一下排序二叉树（BST）是啥。排序二叉树，显然要是一个二叉树。每个节点上有一个 $val$，这棵树的中序遍历是不降的。也就是说，一个节点的左子树中所有的节点的 $val$ 都小于等于这个节点的 $val$，而它的右子树中所有节点的 $val$ 都大于这个节点的 $val$。于是，可以在 ${O}(\texttt{树高})$ 的复杂度内完成许多操作，比如查询第 $k$ 大的 $val$、查询小于 $k$ 的 $val$ 的个数。

考虑如何做这些操作（均设当前节点为 $p$）：

插入 $val$：从根开始向下找，若 $p_{val}<val$，则递归至右孩子。否则递归至左孩子。当 $p$ 为空时，新建节点。
找到第 $k$ 大的 $val$：维护前每个节点的子树大小。从根开始向下找，如果左孩子子树大小大于等于 $k$ 时，递归至左孩子。如果左孩子子树大小等于 $k-1$，则返回当前节点的 $val$。否则，将 $k$ 减去左孩子子树大小再减去 $1$（当前节点），并递归右孩子。
其它也类似，大概就是从根开始，根据一些信息来判断向左或向右递归，再去做些操作。

具体实现时，可以用指针表示左右孩子，可以用成员函数来写，也可以用下标表示，可以用普通函数写。建议用下标表示孩子，并用结构体封装节点，用引用来操作（即代码中的 node &p=tr[rt];）。
可以做 Luogu P5076。

一部分 Code

struct node {
    int val;
    int siz; //本子树大小
    int lc, rc; //左右孩子编号，0 为无孩子 
} tr[N];
void upd(int rt) {
    if(!rt) return;
    node &p = tr[rt];
    p.siz = tr[p.lc].siz + 1 + tr[p.rc].siz;
}
int find_val(int rt, int k){//找到第 k 大的 val
    if(!rt) return -1;
    node &p = tr[rt];
    if(tr[p.lc].siz+1 > k) return find_val(p.lc, k);
    else if(tr[p.lc].siz + 1 == k) return p.val;
    else return find_val(p.rc, k - tr[p.lc].siz - 1);
}

int find_num(int rt, int k){//小于 k 的 val 的个数 
    if(!rt) return 0;
    node &p = tr[rt];
    if(p.val < k) return find_num(p.rc, k) + tr[p.lc].siz + 1;
    else return find_num(p.lc, k);
}

int find_pre(int rt, int k){//小于 k 的最大值
    if(!rt) return −2147483647;
    node &p = tr[rt];
    if(p.val < k) return max(p.val, find_pre(p.rs, k));
    else return find_pre(p.ls, k);
}

int insert(int rt, int val){
    if(!rt) return tr[++cnt] = node{val,1,0,0}, cnt;
    node &p = tr[rt];
    if(p.val < val) p.rc = insert(p.rc, val);
    else p.lc = insert(p.lc, val);
    upd(rt);
    return rt;
}

其它的也都易于实现。但显然的，如果连续插入严格升序的 $val$，复杂度是 $O(n^2)$ 的。于是，需要降低树高。
平衡树是什么？平衡树就是比较平衡的 BST，每个节点左子树大小和右子树大小差不多（非严格定义）。设一个平衡树共 $n$ 个节点，那显然树高是 $\mathrm{O}(\log n)$ 级别的。那么如何把 BST 搞平衡呢？很简单，将每个节点再赋一个随机的 $pri$，使得每个节点的父节点的 $pri$ 比它大，也就是说按 $pri$ 就是一个大根堆（小根堆也可以）。这样的树高期望就是 $O(\log n)$ 的了。作者不太会证明。

然后思考如何插入。
（以下为 Treap 的分裂合并式讲解）
此时，可以发现，这颗树可以分裂成两棵有序的树。可以按 $val$ 分裂（小于 $val$ 的在左，其余的在右），也可以按树的大小分裂。

Code

struct pir { int a, b; }; //a和b含义 把一个树裂成两个之后的树根编号，0 则为空
pir split_val(int rt, int val) {
    if(!rt) return pir{0, 0};
    node &p = tr[rt];
    if(p.val < val) {
        pir o = split_val(p.rs, val);
        p.rs = o.a; o.a = rt; upd(rt);
        return o;
    } else {
        pir o = split_val(p.ls, val);
        p.ls = o.b; o.b = rt; upd(rt);
        return o;
    }
}

pir split_rk(int rt,int k) {
    //如上易得。分裂后左树的大小为 k。
}

也可以发现，如果有两个有序的树（左边的树中最大值小于等于右边的最小值），可以把它们合并。由于树有序了，所以合并时只需要考虑 $pri$ 的大小。$pri$ 较大的放在根，并将某一边的子树和另一个合并。

Code

int merge(int a, int b) {
    if(!a || !b) return a + b;
    node &pa = tr[a], &pb = tr[b];
    if(pa.pri > pb.pri) {
        pa.rs = merge(pa.rs, b);
        upd(a); return a;
    } else {
        pb.ls = merge(a, pb.ls);
        upd(b); return b;
    }
}

如果要插入一个值，就直接将树按这个值裂开为两个，设较小的为 $a$，较大的为 $b$，再新建一个单独的节点表示所插入的值。之后将 $a$ 和这个节点合并，再合并上 $b$ 就行。

Code

int insert(int rt, int val){
    pir o = split_val(rt, val);
    tr[++cnt] = node{val, rand(), 1, 0, 0};// val, pri, siz, lc, rc
    o.a = merge(o.a, cnt);
    return merge(o.a, o.b);
}

其余的没什么变化。也可以将各个查询都按分裂，取出节点再合并的方式进行，但是常数会大些，也不很好写。
同时，由于可以分裂合并，Treap 可以维护（单个或多个）序列。$val$ 就是所谓的 $i$。但是为了在中间插入，可以直接舍弃掉 $val$ 而按照大小分裂。这时某个节点的排名就是 $i$。序列的信息可以储存在每个节点中，由此也可以实现区间加，区间翻转，区间平移之类的操作。类似于线段树，都是打一个 tag，并下传。

区间翻转 Code

//需要一个tag表示是否翻转，同时 pd 函数应该在所有向下找的函数中使用，类似于线段树的 push_down
void pd(int rt){ 
    if(!rt) return;
    node &p = tr[rt];
    if(!p.tg) return;
    if(p.ls) {node &ls = tr[p.ls]; ls.tg ^= 1; swap(ls.ls, ls.rs); }
    if(p.rs) {node &rs = tr[p.rs]; rs.tg ^= 1; swap(rs.ls, rs.rs); }
    p.tg = 0;
}
void revers(int l, int r){
    pir o = split_rk(rt,r),v = split_rk(o.a, l-1);
    node &p = tr[v.b];
    p.tg ^= 1; swap(p.ls, p.rs);
    o.a = merge(o2.a,o2.b);
    rt = merge(o.a,o.b);
}

你甚至可以使用 Treap 来维护环。它与维护序列类似，但需要分类讨论，断开哪里连接哪里，也需要维护一级祖先节点，用来按某个节点分裂。
放个维护序列的典型题：Luogu P2042 [NOI2005] 维护数列。希望你能在 1 天中写完并调完它。（附区间最大子段和维护方式（线段树）：Luogu P4513。这东西在某次 CSP 初赛也出现过。）
其它例题：Luogu 模板题，[NOI2021] 密码箱。